MLA（Multi-Layer Attention） 与 MHA（Multi-Head Attention）的本质区别

MLA（Multi-Layer Attention）和 MHA（Multi-Head Attention） 都是注意力机制的实现，但在架构设计和工作方式上有显著的区别。

以下是对二者的对比和 MLA 的创新之处的详细解析：

1. 核心概念

MHA（Multi-Head Attention）

概念：MHA 是 Transformer 中的标准注意力机制，它将输入的 Query（Q）、Key（K）、Value（V）分成多个头（Heads），每个头独立计算注意力权重，最后将结果拼接起来进行线性变换。

优点：

不同的头可以学习不同的关注模式，增加模型的表示能力。

通过并行计算多头，可以高效处理复杂的上下文关系。

MLA（Multi-Layer Attention）

概念：MLA 通过引入 多层次的分解结构（层内和层间的分解），同时在注意力计算中复用层次间的信息，减少了冗余计算。

优点：

更高的计算效率：通过层次化设计，避免了对每一层重复计算完整的注意力矩阵。

内存友好：对输入进行层次化表示，降低内存占用。

2. 本质区别

特性	MHA（传统多头注意力）	MLA（多层次注意力）
计算方式	每个头独立计算完整的注意力矩阵。	将注意力计算分层处理，复用跨层信息。
计算效率	多个头的并行计算可能导致计算冗余，特别是头数量较多时。	分层机制减少了重复计算，大幅提升效率。
内存需求	每个头都需要存储完整的 Q、K、V 矩阵。	通过跨层次信息复用，降低矩阵存储需求。
关注模式	不同的头学习不同的关注模式，但相互独立。	不仅关注模式多样，还能通过层次间的信息共享增强表示能力。
设计目标	提高模型表示能力，通过多个头捕捉不同特征。	平衡模型效果和计算成本，注重高效推理。

3. MLA 的创新点

层次化分解：

MLA 不再为每个头独立计算注意力矩阵，而是引入多层次分解，将计算任务分配到不同的层。 这种分解方式既保留了模型对上下文的建模能力，又避免了重复计算，极大地提升了效率。 跨层复用：

MLA 允许层与层之间共享部分计算结果，例如在低层次的注意力权重可以直接为高层次提供初始信息。 这种复用机制减少了计算开销，同时提高了上下文信息的一致性。 适配推理与训练：

MLA 在训练时使用高效的分层结构，显著减少梯度计算的复杂性。 在推理时，通过跨层复用优化内存和计算资源使用，使其非常适合大规模推理任务。

MoE

MoE（Mixture of Experts） 是一种稀疏神经网络架构，旨在通过动态激活部分模型参数来提高计算效率和模型性能。MoE 以其在大规模模型中的应用而广受关注，例如在语言建模和多任务学习中的表现。

MoE 的核心概念

Expert（专家模块）：

模型由多个专家模块组成，每个模块可以被视为一个独立的子神经网络，用于处理特定类型的输入。 专家模块的数量可以非常大，但在每次前向或反向传播时，只有少数几个模块会被激活。

Gate（门控机制）：

Gate 是一种选择机制，用于根据输入特征动态选择需要激活的专家模块。 通常使用稀疏门控函数（如 Softmax 或 Top-k）来决定每次只激活少量专家。

稀疏性：

通过稀疏激活，MoE 大幅降低了模型的计算量和内存需求，同时保留了大模型的表示能力。

MoE 的主要特点

计算效率高：

由于每次只激活少量的专家模块，大部分参数不会参与计算，从而降低了计算成本。

参数规模大：

MoE 模型的总参数量可以非常庞大（甚至达到千亿、万亿级），但计算开销相对较小，因为稀疏激活减少了实际参与运算的参数数量。

动态路由：

每个输入都会经过 Gate 机制，动态选择最适合的专家模块。这种灵活性使得 MoE 在多任务和多样性输入场景下具有优势。

MoE 是一种稀疏、动态的神经网络架构，结合了高效性和灵活性。它在提升模型规模、降低计算成本方面具有显著优势，但也面临门控机制优化和分布式训练的技术挑战。随着更多创新（如共享专家、细粒度专家分割）的引入，MoE 的应用前景将更加广阔。

Mixture of Experts（MoE）从诞生到现在，经历了多个关键发展阶段和技术突破。以下是 MoE 在理论提出、实际应用和优化改进中的重要节点：

1. 理论起源：Soft Mixture of Experts（1991） 论文：《Soft Mixtures of Local Experts》（1991，Jacobs et al.） 内容：首次提出 Mixture of Experts 概念，主张用多个子模型（专家模块）处理不同的输入区域，并通过门控机制（Gate）动态选择适合的专家。 贡献： 提出 稀疏激活 和 动态路由 的基本思想。 设计了通过 Softmax 门控动态分配任务的框架。 意义：奠定了 MoE 作为稀疏模型的理论基础。

2. Google 的 GShard 框架（2020） 论文：《GShard: Scaling Giant Models with Conditional Computation》（2020，Google） 内容：在大规模语言模型中使用 MoE 架构，通过分布式训练和稀疏激活解决了超大模型的计算瓶颈。 关键技术： 提出 专家分组（Expert Partitioning） 和 动态专家路由。 使用分布式训练策略，支持数百亿参数的 MoE 模型。 意义： 将 MoE 从理论研究带入实际应用，尤其是在 NLP 任务中的大规模模型。

3. Switch Transformer（2021） 论文：《Switch Transformers: Scaling to Trillion Parameter Models with Simple and Efficient Sparsity》（2021，Google） 内容：提出了一种更简单的 MoE 实现，每次只激活一个专家，显著降低了计算复杂度。 创新点： 单专家激活：相比 GShard 的多专家激活，Switch Transformer 进一步减少了计算成本。 门控机制改进：引入负载均衡损失，缓解专家不均衡问题。 效果： 在 NLP 任务中实现了超越 GPT-3 的性能，同时推理成本更低。 支持万亿参数规模模型。 意义：将 MoE 推向主流模型架构，奠定了稀疏激活技术的地位。

4. DeepSpeed MoE（2021） 工具：《DeepSpeed-MoE: Advancing Mixture of Experts (MoE) Training and Inference》（2021，Microsoft） 内容：推出了开源的 MoE 训练框架，支持超大规模分布式模型的高效训练。 关键技术： 稀疏训练优化：优化了稀疏门控和专家路由的效率。 动态内存分配：降低内存占用，提升了 GPU 资源利用率。 分布式推理：在大规模推理任务中实现高效专家调度。 意义： 为研究人员和企业提供了实用的 MoE 训练工具，推动了 MoE 的广泛应用。

5. Mixtral MoE（2022） 论文：《Mixtral: Balancing Sparsity and Generalization in Mixture of Experts》（2022） 内容：探索稀疏激活与模型泛化能力之间的平衡，提出了一种结合传统和稀疏专家的新框架。 关键技术： 引入部分专家共享机制，提高专家模块的参数利用率。 将部分稀疏专家替换为密集模块，增强模型的泛化能力。 意义：解决了稀疏激活模型在某些任务中的泛化问题。

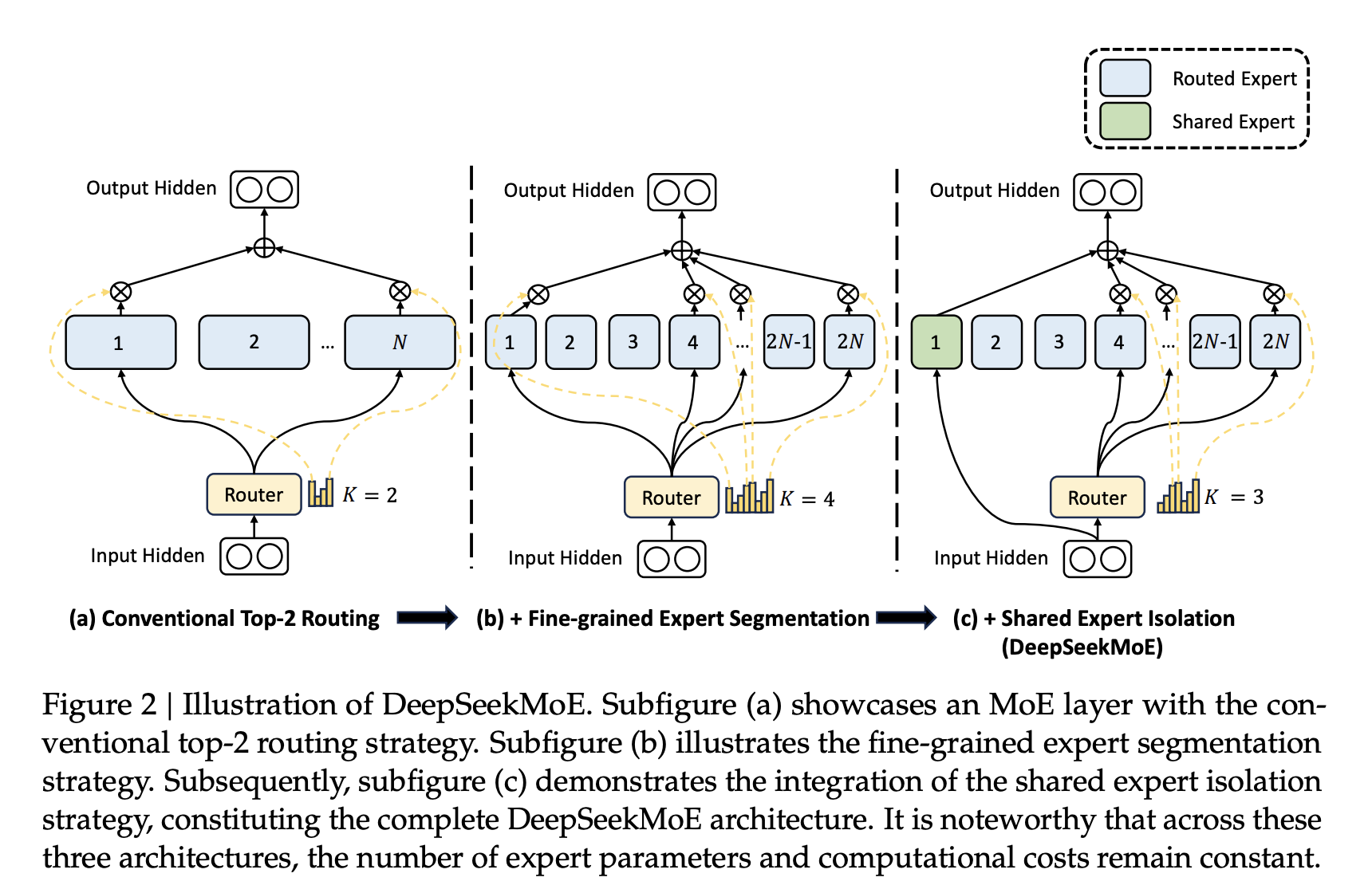
6. DeepSeekMoE（2023） 创新概念：引入 共享专家 和 细粒度专家分割，改进 MoE 框架。 内容： 共享专家：多任务共享部分专家模块，减少了参数冗余。 细粒度分割：将专家模块进一步划分，动态选择更精确的计算单元。 意义：使 MoE 在多任务学习中的表现更高效，同时进一步降低推理成本。

7. Sparse MoE 的未来发展

趋势：

超大规模模型优化：继续提升万亿参数模型的稀疏激活效率。 低资源设备适配：优化 MoE 架构，使其在低内存设备上运行。 多模态融合：将 MoE 架构应用到多模态任务中（如图像、文本联合建模）。

总结

从 1991 年的基础理论到如今的超大规模稀疏模型，MoE 在效率提升和应用场景中不断演进。以下是其关键发展节点：

1991：理论起源（Soft Mixture of Experts）。 2020：GShard 推动大规模分布式应用。 2021：Switch Transformer 提高效率，广泛应用。 2021：DeepSpeed MoE 提供开源工具。 2022：Mixtral MoE 探索稀疏与泛化的平衡。 2023：DeepSeekMoE 引入共享专家与细粒度优化。

MoE 未来将在更高效的推理、更广泛的多模态应用中发挥重要作用。

其他

Floating point 32

四位量化

import numpy as np


def quantize_weights(weights, bits=4):
    # 1. 确定权重范围
    w_min, w_max = weights.min(), weights.max()
    scale = (w_max - w_min) / (2 ** bits - 1)  # 量化步长

    # 2. 量化
    quantized = np.round((weights - w_min) / scale).astype(np.int8)

    # 3. 存储缩放参数
    return quantized, scale, w_min


def dequantize_weights(quantized, scale, w_min):
    # 反量化
    return quantized * scale + w_min


# 示例
weights = np.array([0.1, 0.5, 1.0, 1.5], dtype=np.float32)
quantized, scale, w_min = quantize_weights(weights)
print("量化结果:", quantized)
print("恢复结果:", dequantize_weights(quantized, scale, w_min))
复制

打印结果：

量化结果: [ 0  4 10 15]
恢复结果: [0.1        0.47333333 1.03333332 1.49999998]
复制