搜索与学习的规模化：从强化学习角度复现 o1 的路线图

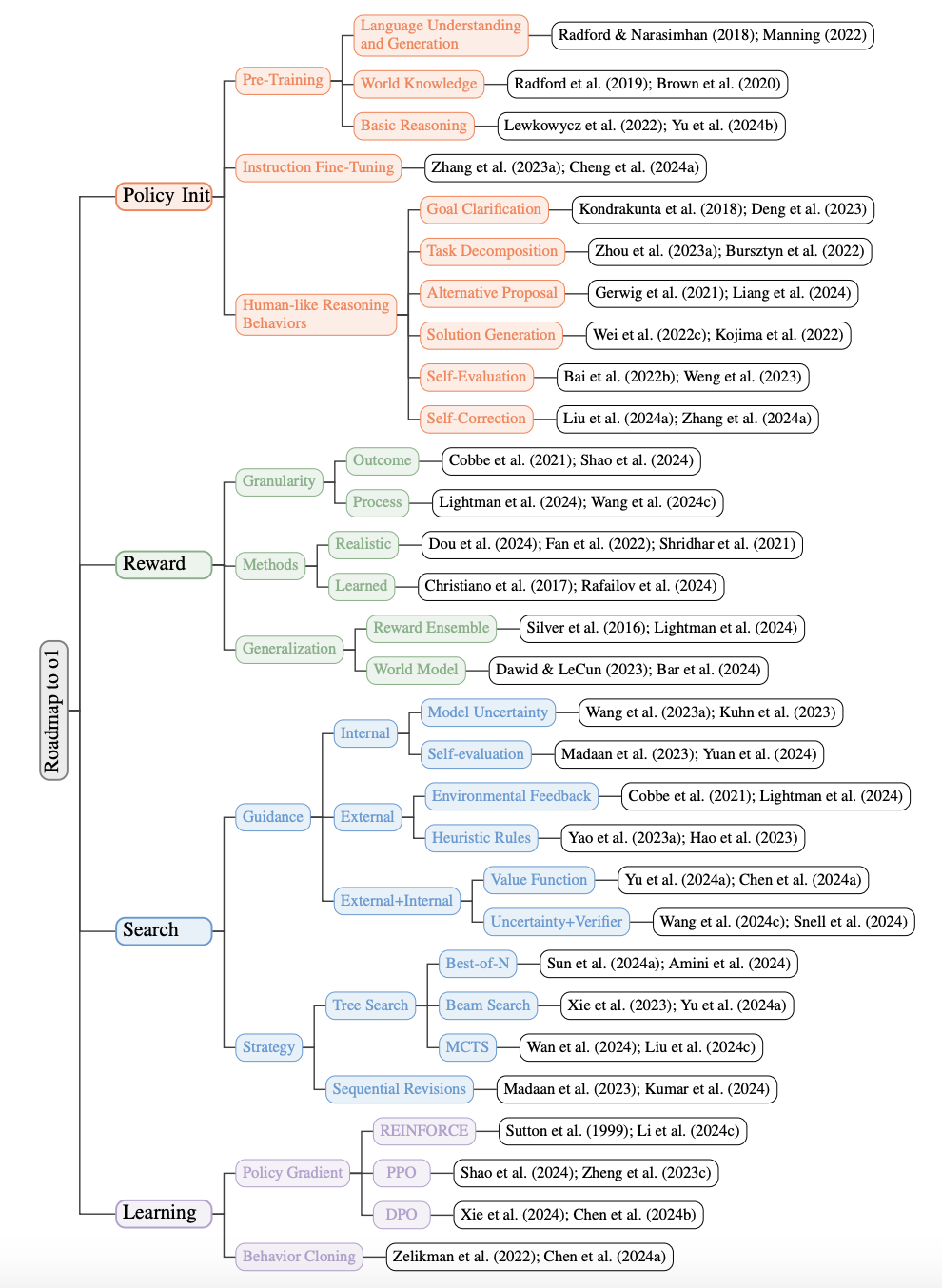
对应论文：https://arxiv.org/pdf/2412.14135

近年来，大型语言模型（LLM）在解决复杂推理任务方面取得了显著进展，而 OpenAI 的 o1 模型 是这一领域的里程碑。它通过强化学习技术，不仅提升了推理能力，还在搜索效率和学习策略上实现了优化。本文将从强化学习的四个核心环节出发：策略初始化、奖励设计、搜索和学习，详细分析 o1 的开发路线图。

1. 策略初始化：构建类人推理能力

1.1 定义与目标

策略初始化的目标是让模型在推理任务中展现出类人的行为，例如：

任务分解：将复杂任务拆分为可操作的子任务。
多样性生成：为同一任务生成多种解答。
自我纠错：在推理过程中识别并修正错误。

这一过程为模型提供了基础推理能力，确保后续搜索和学习的效率。

1.2 关键技术

预训练（Pre-training）
- 使用大规模文本语料（如百科、代码库）训练语言模型，培养基本的语言理解和表达能力。
- 方法：基于 Transformer 架构，采用自回归任务（GPT）或掩码任务（BERT）。
监督微调（Supervised Fine-tuning）
- 在领域数据集上进一步优化，让模型专注于特定任务。
- 例如：通过高质量人类标签数据让模型学习数学推导、编程逻辑等。
任务分解策略
- 逐步推理（Step-by-step Reasoning）：引导模型分步解决问题。
- 推理链（Chain-of-Thought Prompting, CoT）：鼓励模型生成逻辑清晰的中间推理步骤。

逐步推理（Step-by-step Reasoning） 和 推理链（Chain-of-Thought Prompting, CoT） 是两种与模型推理能力相关的技术，它们的目标相似，但实现方式和侧重点存在差异。

逐步推理（Step-by-step Reasoning）

核心思想：将问题分解为若干简单的子任务，让模型逐步完成这些子任务以解决整体问题。
实现方式：通常通过外部的逻辑设计（如将问题拆解为多个步骤）或任务框架分割，逐步输入模型处理每个步骤。
特点：
- 偏重于任务的结构化设计。
- 依赖外部对问题的预处理（如问题分解）。
- 每一步处理时可能是相互独立的。
适用场景：复杂问题（如多步计算、依赖上下文的任务）需要人工设计明确的分解规则。

示例：输入问题：计算 (2+3) × (4-2) + 5 逐步拆解：

第一步：计算 2+3，得到 5。
第二步：计算 4-2，得到 2。
第三步：计算 5 × 2，得到 10。
第四步：计算 10 + 5，结果为 15。

逐步推理是设计一种解题流程，让模型分别处理每一步。

推理链（Chain-of-Thought Prompting, CoT）

核心思想：通过提示词（Prompt）的设计，让模型在生成答案时显式地展现中间推理过程，逐步得出最终答案。
实现方式：利用自然语言提示引导模型生成逻辑连贯的中间步骤，避免直接给出最终答案。
特点：
- 强调逻辑清晰的推理链条。
- 完全依赖模型内在的推理能力。
- 不需要外部问题分解，模型自主生成中间步骤。
适用场景：开放性问题（如推理类问答、数学问题）中，需要模型在没有明确分解规则的情况下推导逻辑。

示例：输入问题：计算 (2+3) × (4-2) + 5 CoT 提示：

1. 首先计算括号内的值：2+3=5 和 4-2=2。
2. 然后计算乘积：5 × 2 = 10。
3. 最后计算加法：10 + 5 = 15。
结果是 15。

推理链是一种提示设计，鼓励模型在回答过程中生成清晰的逻辑步骤。

特点	逐步推理（Step-by-step Reasoning）	推理链（Chain-of-Thought Prompting, CoT）
核心方法	人为分解任务并逐步输入模型	通过提示引导模型生成逻辑清晰的推理链条
实现依赖	依赖外部预处理逻辑和明确的分解规则	依赖提示设计和模型的内在推理能力
是否显式过程	每一步是显式独立处理	中间推理步骤是显式生成的一部分
任务设计复杂度	高：需要人为构造分解流程	较低：通过 Prompt 即可实现
适用场景	数学运算、规划任务等需明确分解规则的任务	推理类问答、开放式问题等逻辑复杂的任务
输出连贯性	各步骤独立，连贯性依赖任务设计	连贯性由模型自主生成

逐步推理和推理链并不矛盾，可以结合使用：

逐步推理提供框架：在明确分解步骤的基础上，要求模型在每一步生成清晰的推理链条。
CoT 提高每步解释性：在逐步推理的过程中，用推理链提示模型解释其每一步的逻辑。

示例：输入任务：解决多步数学问题。

逐步推理：外部将问题分解为子问题。
推理链：在每个子问题中，通过提示生成详细的推理步骤。

这种结合方式能同时利用人工设计的分解规则和模型内在的推理能力，提升解决复杂问题的效率和解释性。

输入：


请计算：(2+3) × (4-2) + 5

通过 Chain-of-Thought 生成的中间步骤：


1. 计算 (2+3) = 5
2. 计算 (4-2) = 2
3. 计算 5 × 2 = 10
4. 最后加上 5，结果为 15

这种分步推理有效提高了推理的可解释性和准确性。

2. 奖励设计：优化目标引导

2.1 定义与目标

奖励设计决定了强化学习过程中的优化方向。对于 o1 模型，奖励信号主要围绕以下目标展开：

完成任务的正确性：确保模型生成准确解答。
解答的效率：鼓励模型以较少计算找到最优解。
生成的多样性与质量：避免单一答案，提升结果的丰富性。

2.2 关键技术

奖励信号设计
- 任务完成度奖励：对正确解答赋予高奖励。
- 质量奖励：根据答案流畅性、逻辑性等综合评估结果。
- 时间效率奖励：限制生成步数，提升搜索效率。
反馈强化学习（Reinforcement from Human Feedback, RLHF）
- 引入人类反馈作为奖励信号，通过强化学习优化模型行为。
- 例如：通过人类标注优选答案，提高模型生成的偏好性。
对抗奖励（Adversarial Reward）
- 设计对抗样本评估模型的鲁棒性，鼓励模型在复杂场景下保持稳定表现。

2.3 示例

奖励函数公式：

R(x) = R_{\text{accuracy}}(x) + \lambda \cdot R_{\text{efficiency}}(x) + \mu \cdot R_{\text{diversity}}(x)

其中：

$R_{\text{accuracy}}(x)$ ：正确性奖励
$R_{\text{efficiency}}(x)$ ：时间效率奖励
$R_{\text{diversity}}(x)$ ：多样性奖励
$\lambda, \mu$ ：权重参数

3. 搜索：高效解答生成

3.1 定义与目标

搜索是 o1 模型提升推理能力的核心环节，其目标是高效探索解答空间，找到最优解。主要包括：

候选答案生成：生成可能的解答路径。
结果筛选与验证：通过评分机制选取最佳解答。

3.2 关键技术

基于树的搜索（Tree-based Search）
- 使用类似蒙特卡洛树搜索（MCTS）的策略，探索多种解答路径。
- 每个分支表示一种推理步骤，最终选择路径评分最高的解答。
启发式搜索（Heuristic Search）
- 引入启发式函数（如置信度分数）优先选择潜在高质量解答。
多路径搜索
- 同时探索多条路径，避免陷入局部最优。

3.3 示例

输入问题：


证明：如果 x 是偶数，则 x^2 也是偶数。

搜索路径示例：

路径 1：假设 x=2n，推导出 $(2n)^2 = 4n^2$ ，显然是偶数。
路径 2：从定义出发，偶数可被 2 整除，验证 $x^2 \mod 2 = 0$ 。

最终根据评分选择路径 1 作为输出。

4. 学习：通过数据迭代优化

4.1 定义与目标

学习是强化学习的核心目标，通过搜索生成的数据迭代优化模型，提升其推理能力和鲁棒性。

4.2 关键技术

监督学习
- 使用搜索生成的高质量答案作为训练数据，更新模型参数。
- 提升模型对特定任务的适应性。
自监督学习
- 利用中间步骤和模型反馈生成更多训练数据，实现无标注数据的有效利用。
对抗训练
- 将搜索过程中生成的错误答案或对抗样本加入训练集，提高模型的鲁棒性。

4.3 示例

输入：


推导：二次方程 ax^2 + bx + c = 0 的解。

模型在第一轮搜索后可能生成多个解：

正确解： $(-b \pm \sqrt{b^2 - 4ac}) / 2a$
错误解：忽略判别式可能小于 0 的情况。

通过训练，模型学会避免生成错误解。

总结

OpenAI 的 o1 模型通过 策略初始化、奖励设计、搜索和学习四个环节，建立了强大的推理能力。这一强化学习路线图不仅为 LLM 的优化提供了重要指导，也为开发下一代智能模型奠定了基础。

如果你对某一环节感兴趣，可以进一步研究相关实现或尝试基于此路线图设计自己的模型！

Jupyter AI

复现 o1 的路线图